À propos de la censure et à propos des marées

Un historique de toutes nos réunions

---

Table des matières

• mercredi 8 août 2018 (précédent)
• mercredi 10 octobre 2018 (suivant)
• Tous les comptes-rendus

mercredi 12 septembre 2018

La voix du secrétaire (Jean)

Présents à la réunion, en fonction de la disposition autour de la table :

• Sébastien,
• Laurent (B),
• moi,
• Sylvain,
• Emmanuel,
• Richard,
• Laurent (R),
• et Hassiba.

Nous avons mangé des nems au poulet, des ravioles, du foie de canard, du chèvre chaud, des bo-buns, de l'andouillette, une entrecôte, des burger (avec ou sans fromage), une crème brûlée et des fondants au chocolat. Nous avons bu des mojitos, des cocktails Diderot, de la bière, du rosé, un café normal et un décaféiné.

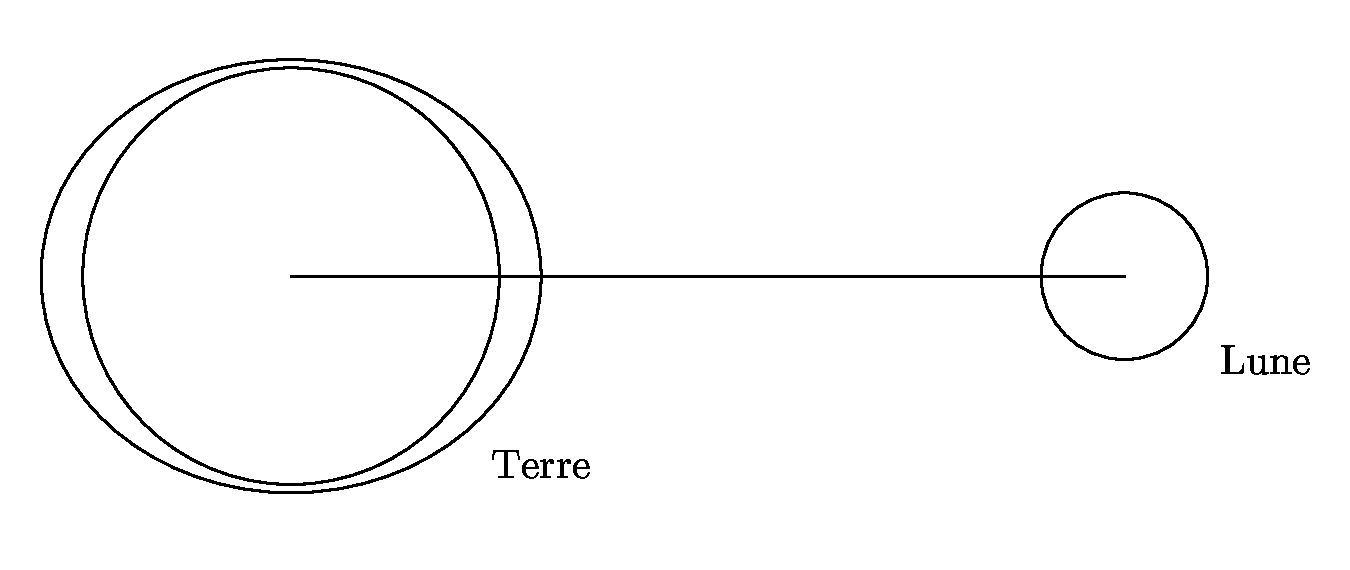
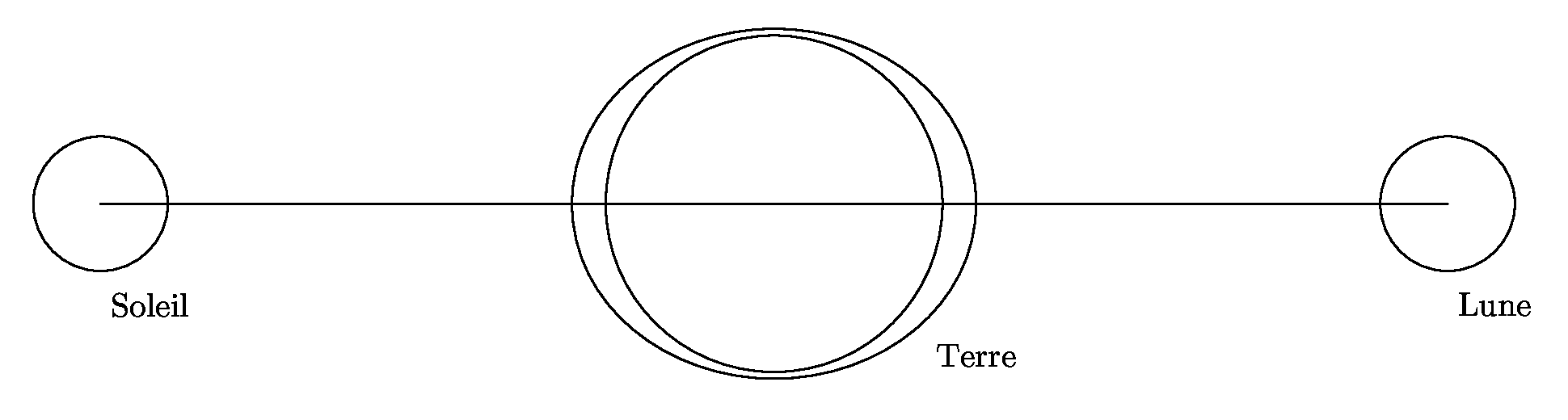
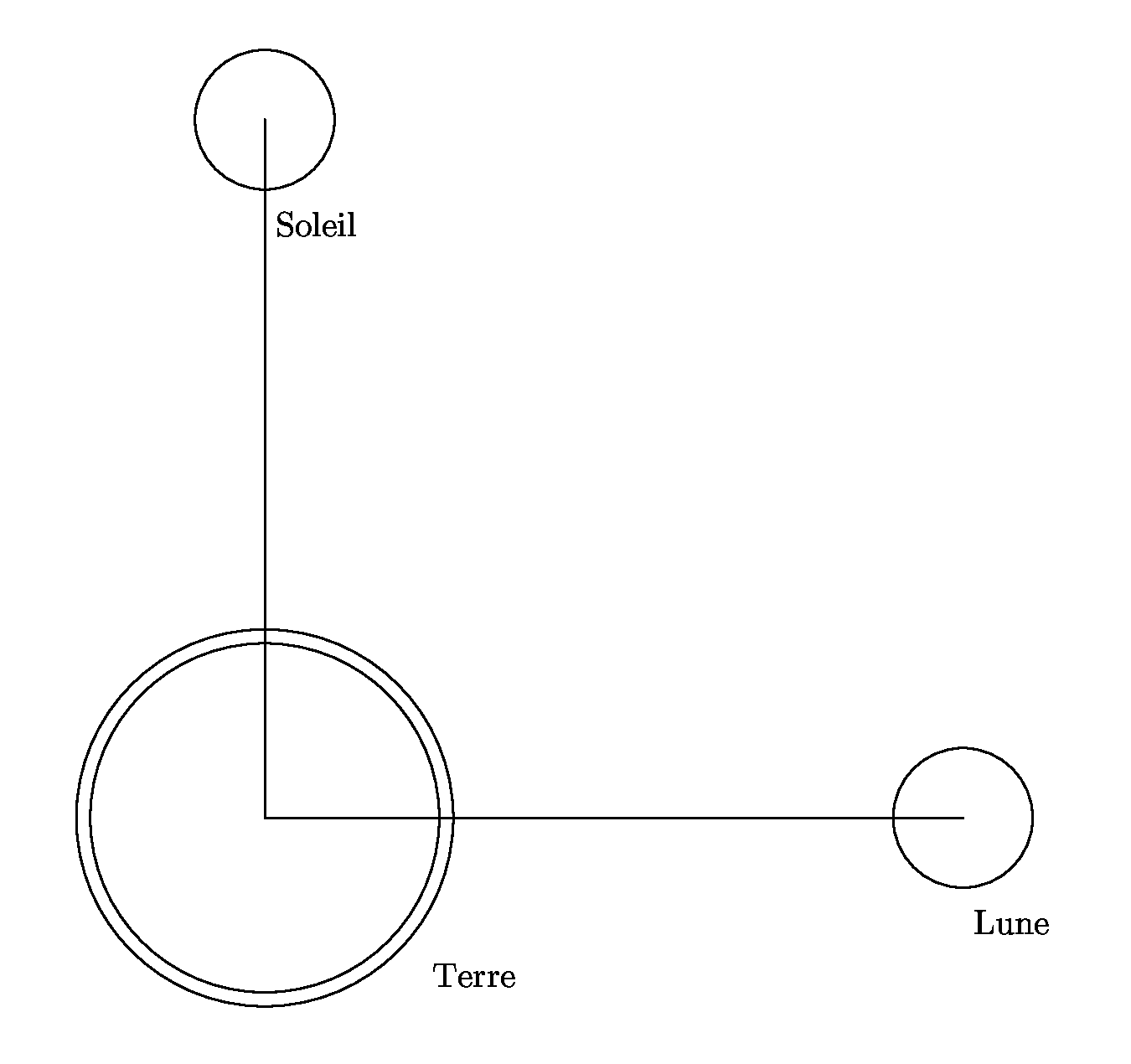
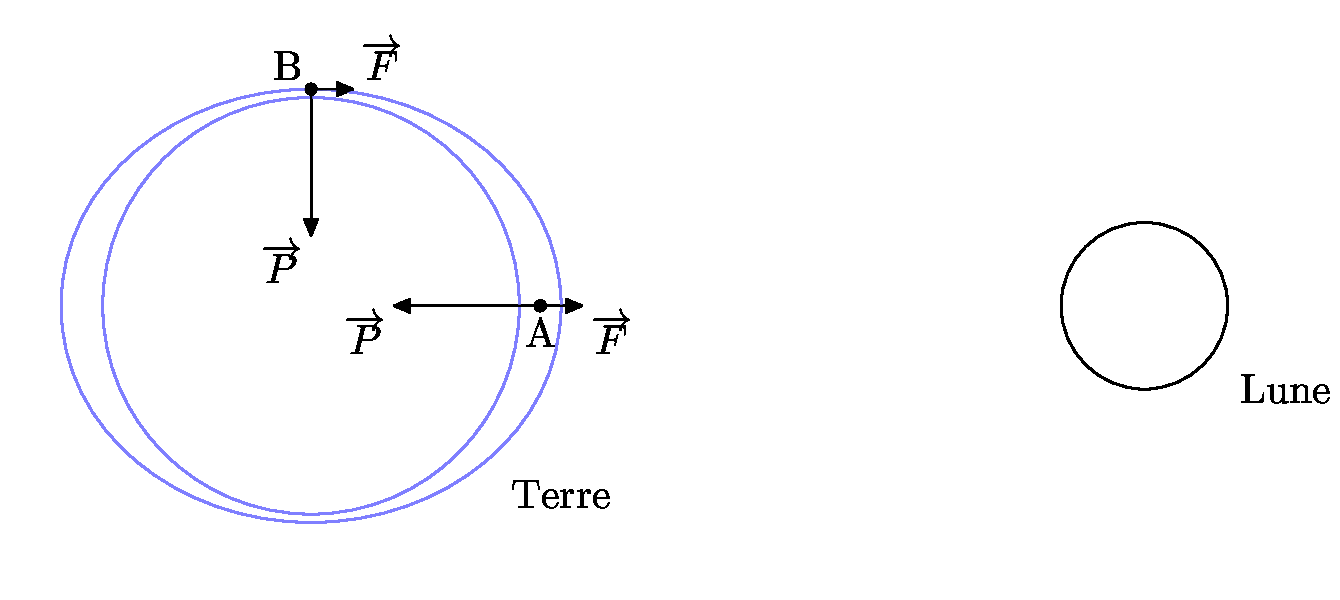
Nous avons parlé de Perl, Internet informatique et points divers. Avec un chapitre particulier sur la censure et le racisme et un autre sur le mécanisme des marées

Perl

• Un élément récurrent lors de la soirée, c'est les caractéristiques de ACT (A Conference Toolkit) version PSGI. Emmanuel tente de constituer des paquets RPM pour Fedora pour les différents modules dont dépend ACT mais il est gêné par toutes les dépendances qu'il découvre au fur et à mesure de ses tentatives. C'est ainsi qu'il a appris le fait que Wiki::Toolkit permet de choisir son moteur de recherche pour le contenu du wiki. Parmi ces moteurs, on retrouve Plucene, une réimplémentation en Perl du moteur de recherche Lucene. Il a aussi créé un paquet pour Template::Multilingual, l'un des rares modules d'Éric sur CPAN.
• À notre connaissance, il existe en tout et pour tout quatre instances d'ACT. Celle des Mongueurs de Perl pour commencer, une dont s'occupe Andrew Shitov, une troisième aux États-Unis et une quatrième au Brésil. Quant aux Japonais, je savais qu'ils avaient eu d'importants problèmes de latence avec notre instance et qu'ils avaient recouru à une autre solution. Je croyais qu'ils avaient installé leur instance d'ACT, mais Sébastien rectifie et me dit qu'ils ont adopté un autre logiciel.
• Dans Perl 5, il existe un point qui déplaît à Sylvain. Dans une chaîne entre doubles quotes, il est possible d'interpoler un scalaire $a (comme en Perl 4), un tableau @b (une nouveauté de Perl 5), mais pas un hachage %c. Ce n'est pas très orthogonal. Sébastien répond que l'interpolation des hachages aurait fait perdre la possibilité de lignes telles que

  printf "Il y a besoin de %d kg de %s\n", $quantite, $ingredient;
  

  Une autre objection, c'est qu'il n'y a pas de façon naturelle de convertir un hachage en chaîne de caractères.
• Lorsqu'il donne des formations Perl ou des cours de Perl, Sylvain répond aux questions des stagiaires ou des étudiants, bien entendu. Avec l'expérience, il a remarqué que c'était à peu près toujours les mêmes questions, avec une particularité. Il y a un jeu de questions récurrentes lorsque les étudiants viennent de la culture Java et il y a un autre jeu de questions récurrentes lorsque les apprenants sont issus d'un milieu PHP, un troisième pour les habitués du shell et un quatrième pour les pythonistes. D'autre part, la plupart des étudiants digèrent sans trop de soucis les variables spéciales $_ (notamment pour les map et les grep) et @_ (pour les sub) mais lorsqu'il est question de tri et des variables magiques $a et $b, nombreux sont ceux qui sont plus dubitatifs au début. En effet, $a et $b ne semblent pas être des variables du langage, mais des variables que le développeur pourrait décider de créer (avec my), ce qui est vrai aussi ! Ces noms $a et $b troublent beaucoup au début mais les apprenants finissent par s'y faire et même apprécier la puissance de la fonction sort. Notons qu'en utilisant une fonction de comparaison avec signature, du genre :

    sub comp_no_case ($$) {
      my ($x1, $x2) = @_;
      lc($x1) cmp lc($x2);
    }
  

  on n'a plus besoin de la magie sur les variables $a et $b.
• Quel est la meilleure appellation pour la conférence ? Laurent (B) trouve que « YAPC » est plus caractéristique et plus distinctif que « TPCiA » suivi de « TPCiG » puis « TPCiR ». Ou alors, pourquoi ne pas adopter l'appellation « Perlcon » ?
• Rappel historique sur TPC et YAPC (avec quand même une information inédite). Au début, O'Reilly a organisé une conférence sur Perl comme il en existait pour d'autres domaines de l'informatique. Cette conférence s'appelait The Perl Conference ou TPC. Le tarif était de l'ordre de 1000 $ pour le ticket de base, sans compter les extras et auquel il fallait ajouter le transport et l'hébergement. Ce tarif élevé empêchait certaines personnalités importantes de la communauté Perl d'assister à TPC. Il a été décidé d'organiser une conférence grassroots, appelée Yet Another Perl Conference avec un tarif nettement moindre, de l'ordre de la centaine de dollars. Puis O'Reilly a élargi TPC à d'autres communautés et a renommé la conférence OSCON (Open Source Conference), abandonnant l'appellation « TPC ». Mais YAPC a continué à s'appeler YAPC. Puis en 2016 ou 2017, les organisateurs de YAPC ont demandé la permission à O'Reilly d'utiliser la dénomination TPC, ce qui a donné TPCiA en 2017. Laurent R nous rapporte avoir entendu de Larry que s'il a fallu attendre 2017 pour récupérer l'appellation « TPC », c'est parce que pendant tout ce temps personne, absolument personne, n'a pensé à faire la demande à O'Reilly.
• Lors des éditions récentes de TPC/YAPC::EU, Wendy tient une table où elle vend des livres et offre divers autocollants, cartes postales et gadgets. Laurent (R) fait remarquer que Wendy vend son livre à un prix inférieur à celui auquel il achète ses exemplaires d'auteur. Cela s'explique par le fait que Wendy achète ce livre en grande quantité, plus que Laurent, bénéficiant ainsi d'une remise quantitative.
• Rappelons que précédemment, O'Reilly était un sponsor de YAPC::EU et que c'était Josette de O'Reilly UK qui installait une table pour vendre des livres.
• Depuis quelques années, les communications éclairs de 5 mn alternent avec des publicités éclairs de 30 s, où l'on annonce qu'une boîte recrute, qu'il y aura une conférence XXX Perl Workshop à telle date et annonces similaires. Hassiba a ainsi eu ses 30 s de célébrité, pour faire la publicité de RPerl. C'est Wendy qui l'a poussée à faire cette annonce.
• Et il y a eu une communication éclair époustouflante. L'orateur a vu passer une question Javascript sur Stack Overflow,

  Est-il possible de trouver un cas où (a== 1 && a ==2 && a==3) s'évalue à "vrai" en Javascript ?

  Il a décidé d'y appliquer ses compétences Perl pour en faire un JAPH. Ceux qui n'ont pas assisté à la conférence ont tout de suite pensé à la possibilité en Perl 6 de stocker plusieurs valeurs dans une variable :

    my $a = 1 | 2 | 3;
  

  (possible en Perl 5 avec Quantum::Superpositions), mais cela ne figurait pas dans l'exposé. L'une des façons consistait à faire un Tie::Scalar et à inclure une incrémentation ++ dans la routine FETCH. Une autre façon consistait à remplacer les comparaisons « == » par des affectations « = » (mais pas, comme je l'ai cru, via un overload).

Censure et Racisme

• Et il y a eu une communication-éclair censurée. Méta-avertissement : le style de mes comptes-rendus, pas seulement celui-ci, comporte plusieurs procédés qui s'apparentent à de l'auto-censure. Et je rapporte ci-dessous des arguments contre l'auto-censure. Ce n'est pas paradoxal. Nous déplorons l'auto-censure dans les discussions directes, en face à face (si l'on peut utiliser cette expression pour les exposés avec plusieurs dizaines de personnes dans l'assistance). En revanche, pour un compte-rendu sous forme de texte, où le lecteur ne bénéficie pas du ton et de la gestuelle de l'auteur, où l'on peut extraire des citations en les dissociant de leur contexte sans que l'auteur en soit averti, où les moteurs de recherche indexent des mots-clés sans avoir aucune compréhension du texte, je préfère prendre des précautions. D'où l'utilisation de certaines périphrases (ce qui rejoint l'adage de programmation « tout problème peut se résoudre en ajoutant un niveau d'indirection »).
• Rappel : lors de la deuxième journée, Mark Keating a fait une annonce pour expliquer qu'une communication éclair de la veille lui avait été signalée comme étant contraire au code de conduite de la conférence. La communication éclair a donc été retirée du site de TPCiG, y compris les transcriptions vidéo.
• Tout d'abord, de quelle communication éclair s'agit-il ? Un fil de discussion sur Reddit semble dire que c'était la communication éclair sur comment foirer une présentation technique. Cela dit, comme vous pouvez le constater en cliquant sur ce lien hyper-texte, cette communication-éclair est encore disponible et elle est basée sur l'auto-dérision sans aucun élément injurieux pour autrui. Dans le fil de discussion de Reddit, une réponse de Dave C laisse supposer qu'il s'agit d'un autre exposé. Ultérieurement, en visionnant les communications éclair sur Youtube et en comparant avec la liste des exposés je pense avoir retrouvé la mention d'une communication éclair qui ne figure pas dans la vidéo. Le fait que Laurent et moi, ainsi que le premier intervenant du fil de discussion Reddit, nous nous soyons trompés sur l'exposé censuré et le fait que même après avoir retrouvé le titre de cet exposé, je ne sois pas en mesure de me rappeler précisément ce qu'il contenait, ces deux faits montrent que nous n'avons pas été marqués, a fortiori nous n'avons pas été choqués par le contenu de cet exposé.
• Et il y a eu un autre incident lors de TPCiG. Les organisateurs ont pensé que l'enregistrement des arrivants irait plus vite si la taille des T-shirts était marquée sur le badge des conférenciers. Éh bien cela n'a pas plu à un participant, qui s'est plaint aux organisateurs. D'où une autre confession et une autre auto-critique de Mark K. dans son intervention du deuxième jour. On peut se demander ce que ce participant voulait garder privé, car sa taille de T-shirt est clairement associée à sa taille et sa carrure, qu'il ne peut pas dissimuler.
• N'importe comment, quoi que les organisateurs fassent, les irascibles et les mauvais coucheurs trouveront toujours à se plaindre. Ainsi, un participant à notre réunion, ne connaissant pas Perl 6 (ou prétendant ne pas connaître) s'est plaint que tous les exposés sur Perl 6 à la conférence constituaient une injure à la face de ceux qui ne connaissent pas Perl 6 et il exige que ces exposés soient retirés des vidéos et de la liste des présentations (c'était un sarcasme, bien sûr).
• Pour évaluer une réflexion, il faut tenir compte de l'auteur de cette réflexion, tant pour sa personnalité que pour son environnement social. Ainsi, nous avons discuté d'une réflexion sur l'équipe française de foot-ball, que quelqu'un a qualifiée d'équipe d'Afrique. L'interprétation et les réactions ne sont pas les mêmes selon que la personne ayant émis cette réflexion est une personnalité française ou, comme c'était le cas dans l'anecdote rapportée, un humoriste sud-africain lui-même de race noire.
• Pierre Desproges et Dieudonné ont tous deux sorti des sketchs qui peuvent choquer certains. Il y a une différence entre les deux, toutefois. Lorsque les caméras et les projecteurs étaient éteints, Pierre Desproges avait des idées et des opinions tout-à-fait neutres et exemptes de racisme, alors que sur scène Dieudonné ne fait que reprendre les opinions qu'il a habituellement, même en dehors de ses spectacles.
• Un autre exemple, avec Georges Brassens. Pour les jeunes générations, une lecture superficielle des paroles de Gare au Gorille pourrait faire apparaître cette chanson comme un texte homophobe. Alors qu'en fait, pour ceux qui connaissent le chanteur, cette chanson est sans conteste un cocktail réunissant les gauloiseries fréquentes chez Brassens et la rébellion contre les institutions et les lois.
• Il faut tenir compte non seulement de la personnalité de l'auteur, mais aussi du contexte historique. Ainsi, Mark Twain utilisait « ze N oueurde » sans aucune arrière-pensée, parce que c'était naturel au XIX^e siècle. De même, lorsque Hergé a publié Tintin au Congo, il a écrit de nombreux gags ridiculisant les noirs, parce que c'était naturel dans les années 1920 et 1930. Depuis, le monde a changé. La réaction des éditeurs de Tintin a été d'ajouter un avant-propos expliquant le contexte historico-culturel de l'album. La réaction de certains américains a été diffuser une nouvelle version revue et corrigée politiquement correcte de les Aventures d'Huckleberry Finn en remplaçant « ze N oueurde » par slave (ce qui ne doit pas plaire aux pythonistes). Certes, cette réédition n'est pas passée inaperçue et a généré de nombreuses réactions, assez souvent négatives, mais cela montre que nous sommes sur une pente glissante.
• Quant à la version française de « ze N oueurde », un participant raconte qu'au lycée, des camarades noirs n'avaient aucune réticence à utiliser ce terme, tandis que lui faisait attention à formuler ses phrases pour éviter ce mot, pour lui trop chargé de connotations négatives.
• Si les éditions récentes de Tintin au Congo ont pris des précautions vis-à-vis du contenu raciste de l'album, il n'y a pas eu tant de précautions avec le Lotus Bleu, qui est tout autant raciste.
• Et pour juger sur le caractère raciste ou non de tel ou tel individu, on peut avoir des surprises. On cite ainsi le personnage joué par Clint Eastwood dans Gran Torino, qui ne peut pas pifrer les asiatiques mais qui, par la force des choses, prend un adolescent asiatique sous son aile et lui apporte son soutien. On cite également un cas similaire dans la vie réelle (en France), un homme qui ne tarit pas en propos racistes. Et pourtant, comme le personnage de Clint Eastwood, il a pris en charge trois jeunes qui auraient sûrement tourné en « kaïra » sans son intervention. Pour couronner le tout, cet homme raciste a une épouse noire et une fille, vous l'avez deviné, métisse.
• En s'éloignant du sujet de la censure, mais en revenant à la fois sur Tintin et les gorilles, il y a un album (Tintin au Congo ?) où un personnage (Tintin ?) est déguisé en gorille. Il y en a un autre, l'Île Noire, où Tintin rencontre un véritable gorille, présenté comme un monstre féroce gardant le château de l'Île Noire.
• Et le sexisme ? On peut remarquer que parmi les personnages de Tintin, la gent masculine est prépondérante. On note toutefois deux personnages féminins importants et récurrents, la Castafiore et sa camériste, Irma. Laurent (B) mentionne une brève apparition de Mme Sanzot, la femme du boucher.
• Le sexisme dans Astérix ? Remarquons d'abord que les personnages féminins sont nettement plus nombreux que dans Tintin. Remarquons ensuite que les gauloises ne sont pas présentées à leur avantage, mais on peut en dire autant de leurs maris. Certains ont cherché comment s'appelait la femme d'Agecanonix. Je précise que jamais dans les albums d'Astérix on ne donne son nom.

Internet

• Il y a quelques années, les grands de la diffusion de musique, de films et mème de livres étaient à fond dans les DRM. Ils ont tendance à se calmer maintenant, car ils ont compris que de nombreux consommateurs possèdent plusieurs appareils (PC, tablette et téléphone) et considèrent que s'ils achètent une œuvre, c'est pour pouvoir la lire, l'écouter ou la visionner sur n'importe lequel de ces appareils.
• Pour la musique, le site le plus connu est Spotify. Il y a aussi Band Camp, qui permet de découvrir de nouveaux talents, ce qui est moins facile si l'on se contente de Spotify.

Informatique

• Alors que Perl a une seule fonction de tri, à laquelle il faut fournir une fonction de rappel (callback) si l'on veut faire quelque chose de particulier, PHP en a 16 (et pas 20 ou 30 comme certains le pensaient). Il y a le tri numérique, le tri alphabétique, le tri alphabétique indépendant de la casse et diverses autres variations. Et sans uniformité sur la règle de nommage ou sur la liste des paramètres attendus. Un site web répertorie toutes ces incohérences. De façon paradoxale, ce site, bien que critique vis-à-vis de PHP, est très souvent visité par les programmeurs PHP, car il présente de façon synthétique et ergonomique les fonctions de tri, contrairement à la documentation officielle de PHP.
• Signalons que c'est Randal Schwartz qui a comparé PHP à « des roues latérales stabilisatrices sans le vélo ».
• Sébastien va suivre une formation à Power Shell. Un intérêt notable de ce langage de commande, c'est qu'il est disponible non seulement sous Windows, mais ausi sous Linux (et d'autres variantes d'Unix ?). Toutefois, Laurent (B) n'est pas intéressé, même s'il est censé déployer des scripts à la fois vers Linux et vers Windows. En effet, Laurent doit agir en faisant aussi peu de suppositions que possible et il n'a ainsi pas le droit de supposer que Power Shell est installé sur toutes les machines cibles. La seule chose acquise, c'est que toutes les machines cibles ont Git. Et comme toutes les installations Git ont bash, Laurent programme en bash.
• Question aux partisans de Linux et à ceux de *BSD. Lorsque votre employeur vous colle une machine Windows, quels logiciels installez-vous ? Laurent (B) installe Firefox puis Cygwin. Quant à moi, j'installe Emacs puis Cygwin.

Divers

• Il a été question d'une chanson de François Valéry, Elle danse, Marie. Cette chason a la même intro qu'une chanson de David Bowie [ laquelle  ? J'ai cru comprendre Billie Jean que j'associe à Michael Jackson. ] Qui a copié sur l'autre ?
• Et y a-t-il réellement eu copie ? Nous rappelons plusieurs cas au cinéma où des scénarios se ressemblent et où il s'agit d'une coïncidence, pas d'une copie.
• Je rappelle les discussions précédentes à propos de la filiation entre Danse avec les Loups, Pocahontas et Avatar, où j'étais d'accord avec ceux qui pensaient que le véritable intérêt d'Avatar, ce n'était pas son scénario, mais ses effets spéciaux. À noter que je n'ai vu aucun de ces trois films.
• Sébastien, lui, voit plutôt Avatar comme une fusion de Pocahontas et d'Aliens et pas seulement à cause de la présence de Sigourney Weaver.
• Il ne faut surtout pas confondre le film de Cameron avec Avatar, le Maître de l'Air (Avatar, the Last Airbender), qui est un dessin animé à la base et qui a donné lieu à un film.
• De retour sur les chansons qui se copient l'une l'autre. Laurent (B) rappelle que la règle adoptée par la SACEM consiste à comparer les huit premières notes des chansons pour savoir s'il y a plagiat. On peut savoir ce que donne cette règle avec All You Need is Love ?
• Je ne sais plus comment nous sommes venus à parler d'origami. Ce que j'ai retenu, c'est que Stéphane G, connu pour Open Food Facts, est également un adepte de l'origami et qu'il a sa chaîne Youtube.

Le mécanisme des marées

• Comme annoncé le mois dernier, Laurent (B) est allé visité l'usine marémotrice de la Rance. Je ne décrirai pas l'aspect technologique, déjà évoquée brièvement le mois dernier. Je m'appesantirai plus sur le mécanisme des marées et les questions que Laurent s'est posées lors de la visite.

Mes Sources

• Tout d'abord, même si je n'ai pas visité l'usine de la Rance, j'ai vu maintes et maintes fois les trois dessins traditionnels censés décrire le mécanisme des marées. C'est toujours les mêmes que l'on retrouve dans les expositions permanentes des sites du littoral, dans les illustrés éducatifs pour enfants, dans les dessins animés à vocation scientifique pour la jeunesse, dans les émissions culturelles, dans les manuels de géographie et même dans certains ouvrages de vulgarisation d'astronomie.
• Et il y a aussi un numéro de Science & Vie assez ancien, qui présentait lui aussi le mécanisme des marées, mais avec un discours assez différent de toutes les sources citées au paragraphe précédent. Hélas, cela fait très longtemps et je n'ai plus cet article à ma disposition. Dans la suite de l'exposé, je mentionnerai à quelques occasions des détails que j'ai tirés consciemment de cet article. Pour les autres éléments, dont je ne cite pas les sources, ils peuvent venir de ma réflexion personnelle, mais ils peuvent également venir de l'article de Science & Vie, transitant par ma mémoire subconsciente.
• D'accord, c'est Science & Vie, ce n'est pas Pour la Science. Si parmi les quelques numéros de Pour la Science que j'ai eu l'occasion de feuilleter, il y en avait eu un décrivant les marées, je me serais empressé de le citer. Mais ce n'est pas le cas. Je n'ai pas trouvé non plus de livre de Jean-Pierre Petit sur ce sujet et j'en suis fort marri.

La description traditionnelle du mécanisme des marées

• Dans les sites et les ouvrages cités, on a toujours le dessin de base décrivant l'influence de la Lune sur les eaux océaniques de la Terre. À cause de l'attraction gravitationnelle de la Lune, une sorte de monticule d'eau, ou une bosse, se forme à l'aplomb de la Lune. On en trouve un autre également aux antipodes. Les deux bosses sont très exagérées dans ce dessin, mais c'est pour donner une idée.
  
• Ensuite, il y a toujours deux dessins, inséparables, pour tenter d'expliquer les marées de vives-eaux et les marées de mortes-eaux. Ces deux dessins font apparaître le Soleil en plus de la Lune. Dans le dessin pour les marées de vives-eaux, le Soleil et la Lune sont en opposition (de part et d'autre de la Terre). Et on nous explique que les bosses d'eau dues au Soleil se combinent avec celles de la Lune en les renforçant. Le même phenomène se produit également lorsque la Lune et le Soleil sont en conjonction (du même côté de la Terre), mais cette situation n'a pas l'honneur de bénéficier d'un dessin. L'autre dessin montre le Soleil et la Lune en quadrature pour nous faire penser que dans cette configuration, les bosses dues à la Lune sont anéanties par les creux dûs au Soleil et vice-versa.
  
  

Les interrogations de Laurent et quelques autres

• Tout d'abord, dans le dessin de base, comment explique-t-on l'existence de la bosse aux antipodes de la Lune ? Avec l'attraction gravitationnelle de la Lune, cela devrait plutôt faire une cuvette, non ?
• La description des marées montre bien qu'il y a deux marées hautes et deux marées basses par jour (ou à peu près). Mais comment se fait-il que dans l'Océan Pacifique, il y ait une seule marée haute et une seule marée basse par jour ? Laurent a posé la question à la personne qui faisait visiter l'usine et il n'a pas eu de réponse claire.
• La question suivante était un peu trop compliquée à formuler en pleine réunion, car comme vous pouvez le voir, elle nécessite une bonne dose de recherche documentaire, ce qui prend du temps même via Internet. Prenons les ports de Saint-Malo et Portsall. Ces ports sont tous deux sur la côte nord de la Bretagne, à la même latitude. La longitude de Saint-Malo est 2° ouest, tandis que celle de Portsall est de 4° 41' ouest. Si la Lune se lève à l'instant T à Saint-Malo, elle se lève à T plus 11 minutes à Portsall. Si elle culmine à T ' à Saint-Malo, elle culmine à T ' + 11 mn à Portsall. Si la marée est haute à T " à Saint-Malo, elle est haute à T " + 11 mn à Portsall. J'ai vérifié en consultant les horaires de marée de Saint-Malo. et de Portsall. Le jour où j'ai écrit ce paragraphe, le 27 septembre. la marée était haute à Portsall à 07h32 et à 19h46, tandis qu'à Saint-Malo, c'était 09h15 et 21h30, soit près de 1 heure et 45 minutes plus tard. Comment ? 1 h 45 mn de décalage et pas 11 mn ? Et en plus la marée haute de Portsall est en avance sur celle de Saint-Malo ?

La réfutation de la description traditionnelle

• Comme je l'ai dit plus haut, les dessins ne sont pas à l'échelle et la hauteur des bosses est exagérée. De combien ? Science & Vie a fait le calcul. Je me souviens que le résultat pour la hauteur de la bosse était en millimètres, mais je ne sais plus si l'ordre de grandeur était « de 1 à 10 mm » ou si c'était « une fraction de millimètre ». Et je ne me souviens plus non plus si l'auteur donnait une explication pour la bosse aux antipodes de l'astre. La faible valeur de la hauteur de la bosse vient du fait qu'au point A, la force d'attraction par la Lune F doit vaincre le poids P, nettement supérieur.
  
• L'article de Science & Vie continuait en examinant la situation au point B. Cette situation est tout autre. La force F n'est plus opposée au poids P. Elle peut donc agir de façon sensible sur l'eau et provoquer un déplacement latéral de cette eau. Certes, au fur et à mesure que la vitesse de l'eau augmente, de nouvelles forces font leur apparition et s'opposent à F (frottements, viscosité, etc.). Leur valeur est toutefois nettement moindre que celle de P.
• L'étude des marées en faisant le bilan des forces et en intégrant à partir des conditions initiales est trop compliquée, nettement plus compliquée que les exercices de physique mettant en jeu juste un ressort et une masselote ou bien un pendule oscillant. Si l'on choisit un repère lié aux côtes, c'est d'autant plus compliqué car il faut tenir compte de la rotation de la Terre sur elle-même, ce qui fait que ce repère basé sur la Terre n'est pas un repère galiléen. Et quand bien même nous pourrions obtenir un résultat, nous serions noyés dans un flot de valeurs numériques détaillées, qui nous empêcherait de percevoir la substantifique moëlle du résultat global. Il faut donc trouver autre chose.

La physique des systèmes harmoniques

• La réponse, c'est l'analyse générique des systèmes harmoniques. Selon mes souvenirs conscients, cela fait suite à une réflexion d'une de mes profs de physique, mais je pense qu'il devait en être question dans l'article de Science & Vie. Après avoir comparé les systèmes ressort + masselote, les pendules oscillants et les circuits RLC (résistance, inductance et condensateur), elle nous avait dit que lorsqu'un système harmonique recevait un signal en entrée sinusoïdal de fréquence f, le système harmonique produisait un signal de sortie sinusoïdal de même fréquence f.
• Une petite précision : il devait y avoir un domaine de validité que je n'ai pas retenu. En effet, prenons le montage expérimental suivant : un violon avec juste une corde « la » (440 Hz), plus un archet actionné par une machine lui communiquant un mouvement sinusoïdal pur et qui frotte sur la corde du violon. Si la fréquence du mouvement et 1 Hz ou 2 Hz, j'imagine que la corde « la » du violon réagira à 440 Hz. Mais si la fréquence du mouvement de l'archet est 400 Hz, la corde réagira à 400 Hz et si la fréquence est 500 Hz, la corde réagira à 500 Hz.
• Les différentes réponses de la corde ne sont pas équivalentes, toutefois. Avec un mouvement de l'archet à 400 Hz ou 500 Hz, la réponse de la corde sera très faible. Avec un mouvement à 430 Hz ou 450 Hz, la réponse de la corde sera nettement plus importante et elle sera maximale si l'archet se déplace à 440 Hz, la fréquence de résonance de la corde.
• Donc, si le signal d'entrée est purement sinusoïdal de la forme

  E = A sin(ω t)

  alors le signal de sortie est

  S = λ.A sin(ω t + φ)

  Si vous préférez travailler avec une fréquence en hertz plutôt qu'avec une pulsation en radians par seconde, voici les formules

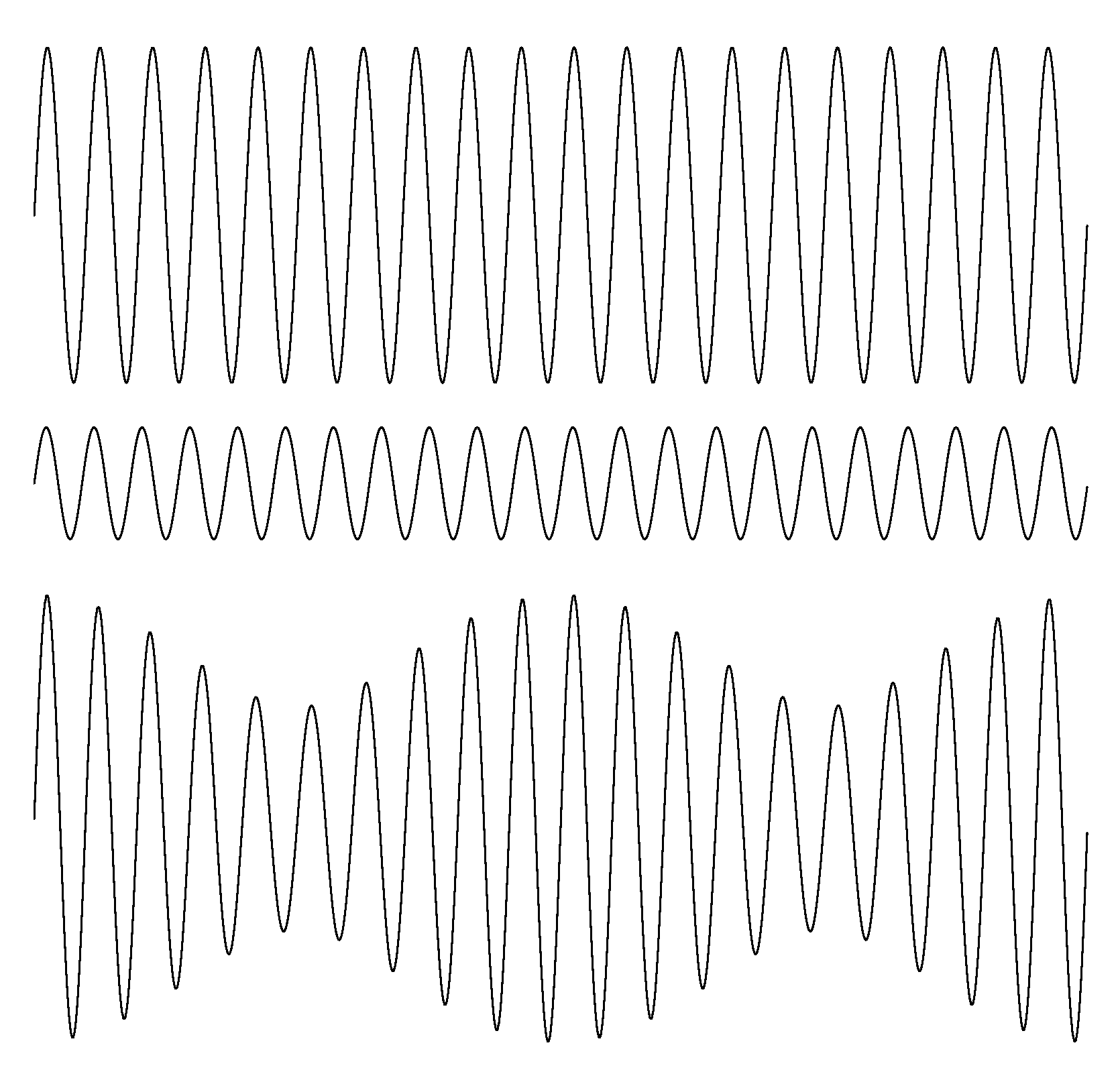
  E = A sin(2 π f t)
  S = λ.A sin(2 π f t + φ)

  Et que se passe-t-il si le signal d'entrée n'est pas sinusoïdal ? Mais quand même périodique ? Attention, nous entrons dans un domaine mathématique que je n'ai pas correctement assimilé, les séries de Fourier (mais c'est encore pire avec la transformée de Fourier et la FFT). On peut décomposer le signal périodique en entrée en composantes sinusoïdales :

  E = Σ_k A_k sin(2 k π f t + ψ_k)

  alors le signal de sortie est

  S = Σ_k λ_k.A_k sin(2 k π f t + ψ_k + φ_k)

  avec λ_k plus ou moins fort selon que la fréquence k f est plus ou moins proche d'une fréquence de résonance du système harmonique.

Application au cas des marées

• La composition de la rotation de la Terre sur elle-même et de la rotation orbitale de la Lune crée un signal périodique à la fréquence f = 11,5 μHz avec, je pense, une composante harmonique à la fréquence 2.f = 23 μHz et des harmoniques supérieurs que j'estime négligeables. Oui, il s'agit bien de microhertz, même si vous êtes habitués aux gigahertz des microprocesseurs. Le signal de sortie est donc

  S = λ₁.A₁ sin(2 π f t + ψ₁ + φ₁) + λ₂.A₂ sin(4 π f t + ψ₂ + φ₂)

  Dans l'Océan Atlantique, la fréquence de résonance est voisine de 23 μHz, donc le coefficient λ₂.A₂ est largement supérieur au coefficient λ₁.A₁ et nous percevons un phénomène à 23 μHz. Dans l'Océan Pacifique, qui a une étendue différente donc une fréquence de résonance différente, plus proche de 11,5 μHz que de 23 μHz, c'est le coefficient λ₁.A₁ qui prédomine par rapport à λ₂.A₂. Les riverains du Pacifique ont ainsi une seule marée par jour.
• Et la Mer Méditerranée ? On dit souvent qu'il n'y a pas de marée en Méditerranée. C'est faux. Il y a des marées, mais très faibles en comparaison avec les marées de l'Atlantique. En Méditerranée, la formule est la même que pour l'Atlantique et le Pacifique, mais les termes λ₁.A₁ et λ₂.A₂ sont beaucoup plus faibles que pour les océans.
• Et les marées de vives-eaux et de mortes-eaux ? Cela découle du phénomène de battements. La présentation traditionnelle des battements consiste à additionner deux signaux sinusoïdaux d'amplitudes strictement identiques et de fréquences f₁ et f₂ voisines. Cela donne ceci :
  
  Le résultat de l'addition donne, pour utiliser le vocabulaire de la radio-téléphonie, une porteuse de fréquence (f₁ + f₂) / 2 avec une modulation d'amplitude de fréquence (f₁ - f₂) / 2 On étudie moins fréquemment le cas de l'addition de deux signaux sinusoïdaux de fréquences voisines et d'amplitudes différentes. Voici ce que cela donne :
  
  On peut le voir, l'étranglement n'est plus absolu, mais il existe quand même. Dans le cas des marées, la fréquence de base du « signal » provenant de la Lune est calculée à partir de la rotation de la Terre sur elle-même et de la rotation orbitale du système Terre-Lune, un tour en 27,3 jours. La fréquence de base du « signal » provenant du Soleil est calculée de la même manière, en combinant la rotation de la Terre sur elle-même et la rotation orbitale du système Soleil-Terre, un tour en 365,25 jours. Les deux fréquences sont voisines, donc l'addition des composantes sinusoïdales des « signaux » en sortie produit des battements. L'étranglement de la courbe correspond à une marée de mortes-eaux et l'endroit le plus large à une marée de vives-eaux.
• Si vous lisez attentivement les pages donnant l'horaire des marées à Saint-Malo. ou à Portsall, vous verrez que l'intervalle entre deux marées hautes ou entre deux marées basses n'est pas constant d'un jour sur l'autre. Donc, le mécanisme n'est pas parfaitement périodique. Je pense néanmoins que les calculs présentés ci-dessus donnent un bon aperçu du phénomène réel.

Conclusion

• Je vous ai rapporté ci-dessus mes réflexions sur le mécanisme des marées. C'est loin d'être une réponse complète sur le sujet, c'est loin d'être rigoureux compte tenu de quelques raccourcis mathématiques auxquels j'ai eu recours. Et finalement, je ne prétends pas être un spécialiste de la question, loin de là. Je vous invite à exercer votre esprit critique, tant vis-à-vis de mes explications que vis-à-vis de la fiction simpliste de la Lune « aspirant » vers le haut une masse d'eau. Peut-être trouverez-vous une troisième explication, plus précise et plus convaincante que la mienne.
• Et pour les illustrations, je vous livre les fichiers sources qui m'ont permis de construire ces schémas avec LuaL^AT_EX et ImageMagick : un document LuaL^AT_EX, les fonctions Lua nécessaires et le script shell qui enchaîne avec ImageMagick.

Post Scriptum

• Pour écrire cette tentative d'explication sommaire du phénomène des marées, je n'ai pas cherché à lire quoi que ce soit sur ce sujet sur Internet. Les seuls points pour lesquels j'ai utilisé Internet sont les horaires des marées de Saint-Malo et Portstall et les valeurs numériques permettant de calculer l'attraction exercée par le Soleil et la Lune sur les objets situés sur la Terre. Pour les marées, j'ai pris soin de me référer uniquement aux sources listées au début de ce chapitre.
• Ultérieurement, j'ai quand même cherché sur Internet si je pouvais trouver des sources confirmant mes conclusions. La plupart du temps, j'ai trouvé l'explication traditionnelle de la bosse attirée par la Lune. J'ai toutefois trouvé (ou on m'a communiqué) quelques sites mentionnant sans ambiguïté les marées comme un phénomène ondulatoire d'un système harmonique. À cette occasion, j'ai appris que mon opinion était confirmée par ni plus ni moins que Pierre-Simon de Laplace et que l'affirmation « dans le Pacifique, il y a une seule marée par jour » est une simplification abusive de la réalité.
• Tout d'abord quelques définitions extraites d'un glossaire composé par quelqu'un de bien connu.
• Ensuite une « brève de maths ».
• Finalement un site qui examine le sujet avec beaucoup plus de détails que ce que j'ai écrit ci-dessus.